By the 18th century, the compass was used only to illustrate the stages of an algebraic proof. Yet two centuries earlier it was still a measuring and drawing instrument used in connection with the theory of proportional sections. It follows that the geometry used by the craftsmen of the past derived from concepts that are no longer familiar to us today.
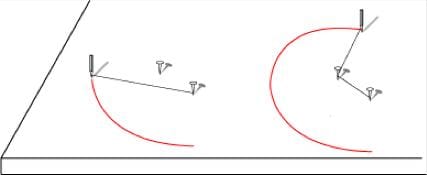
The string-and-pin technique summarises the general idea
of drawing with a compass: "to change the direction of a curve it is sufficient
to add or subtract the measure of a radius from the preceding radius…"
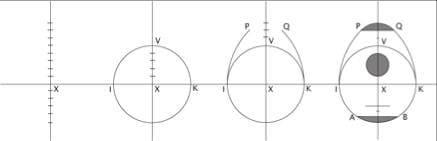
In mediaeval times, the process of measurement
the drawing of a outline was bound to the process of measurement
and the two couldn't be decoupled.
A form is generally described from the division of a line
(here, Henri-Arnaut de Zwolle's lute). In fact, these simple measurements
conceal a relatively elaborate mathematical system based on proportional relations
(below, Zwolle's lute and the proportions of the quadrature of the square
which are the key to its measurements).
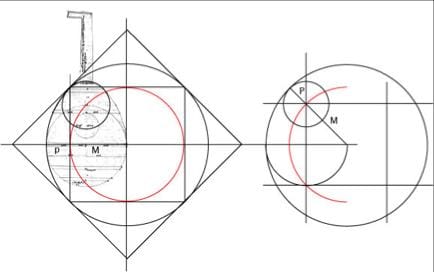
The approximations of irrational values in use before the development of numbering systems are required to interpret these drawing and measurement processes.
These computational techniques, now superseded, lead to the establishment of a link with the notion of analogy (analogia) as the founding principle of an infinite variety of measurements that are "approximately" proportional. From this standpoint, strict proportion illustrates in an educational way an exemplary and ideal structure (the exempla) from which stems the world of copies (analogues) that surround us.
The linked animation Anime Guarneri gives an insight into how these procedures were used in practice. The simple ratios of the various parts belong to the series of numbers which, two by two, approximate the geometric and harmonic sections. The Traité de Lutherie provides the essential foundations for understanding the instrument's form.