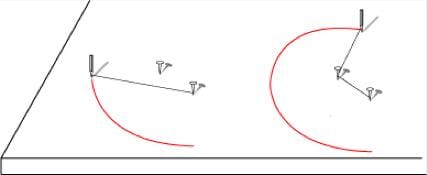
Au XVIII° siècle, le compas ne servait plus qu'à illustrer les étapes d'une démonstration algébrique. Pourtant, deux siècles auparavant, il était encore un instrument de mesure et de dessin en relation avec la théorie des sections proportionnelles. Il s’ensuit que la géométrie des artisans du passé s’était développée à partir de concepts qui ne nous sont plus familiers.



Le tracé à la ficelle résume l'idée général du tracé
au compas: "pour changer la direction d'une courbe il suffit
d'ajouter ou retrancher la mesure d'un rayon au rayon qui précède..."




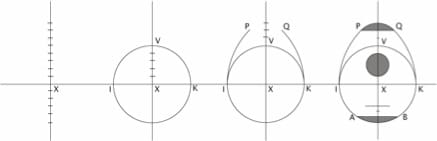
À l'époque médiévale, le dessin d'une forme se confond avec ses mesures.
Il est généralement décrit à partir de la division d'une droite.
En réalité, ces mesures simples dissimulent une pensée mathématique
relativement élaborée fondée sur les sections proportionnelles.
(ci-dessous, le luth de Zwolle et les proportions de la quadrature du carré qui sont la clé de ses mesures)




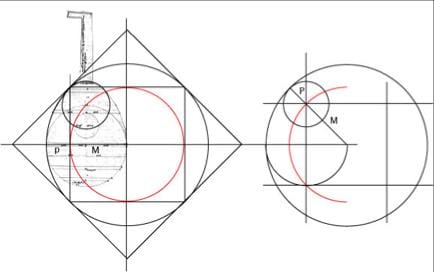
L'interprétation de ces procédés de tracés et de mesures fait appel à des approximations des valeurs irrationnelles.

Ces techniques aujourd'hui disparues, introduisent la notion d'analogie (analogia) en tant que principe à l'origine de la diversité des mesures dites "proportionnelles".


L'animation ci-jointe viola Guarneridonne un aperçu de la mise en œuvre de ces procédures. Les rapports simples des différentes parties appartiennent aux séries des nombres qui deux à deux approchent les sections géométriques et harmoniques. Le Traité de Lutherie fournit les bases essentielles nécessaires à la compréhension de la forme des instrument.